BQ#7: Difference Quotient

1.To find the difference quotient we have to get a graph. Then though that graph we draw a line that touches the graph at two point and we call that the secant line. The coordinate for point A(the first point) is (x,f(x)) and point B has coordinates of (x+h,f(x+h)). We need to calculate the slope of the secant line by slope formula which is y2-y1/x2-x1. Y2=f(x+h), Y1=f(x), X2=x+h, X1=x. The equation should be f(x+h)-f(x)/x+h-x. The x's at the bottom cancel leaving the slope to be f(x+h)-f(x)/h, which is the difference quotient formula.

http://cis.stvincent.edu/carlsond/ma109/diffquot.html

http://simple.wikipedia.org/wiki/Difference_quotient

BQ:#6: Unit U Concept 1-7

1. Continuity/Discontinuities:

-A continuous function is predictable. It has no breaks in the graph, no holes, and no jumps. it can be drawn with a single unbroken pencil stoke and it makes a good bridge.
-A discontinuous function can have 3 types of discontinuities, which are in two families. The two families are removable and non-removable discontinuities. In the removable discontinuities there is a Point discontinuity(known as A Hole). In the non-removable discontinuity family there are: jump discontinuities, oscillating behavior, and infinite discontinuities. They are in two families because Removable discontinuities have limits and non-removable discontinuities do not have limits.

Removable discontinuities:

https://centralmathteacher.wikispaces.com/file/view/math1.JPG/30652173/math1.JPG

Non-removable discontinuities:

http://www.math.brown.edu/utra/discontinuities%205.gif

2. Limits:

-A Limit is the intended height of a function. Sometimes the value of a limit is just approached, meaning the graph never reaches it. A limit exist as long as the height is reached from the left and the right. The right hand limit and the left handed limit must be the same. If a graph does not break at any given x-value then a limit exist. A limit can exist even if the destination is a hole in the graph.
-A limit does not exist at three non-removable discontinuities, which are: comparing left and rgiht behavior, unbounded behavior, and oscillating behavior. When comparing left and right they both must approach the number. If the left-handed limit and the right-handed limit are not the same then the limit does not exist. One-handed statements must be written explaining how the left and the right are not the same. Unbounded Behavior exist because of vertical asymptotes. Having vertical asymptotes makes the function approach infinity from the right and negative infinity from the left. When the limit is unbounded because infinity is not a real number. Oscillating behavior is very wiggly at the origin. This type of function does not have a limit because it doesnt approach any single value.

 Left and right Limit notation:

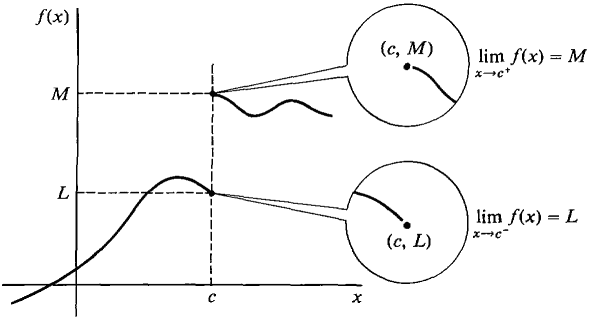http://www.vias.org/calculus/img/03_continuous_functions-69.gif

Unbounded Behavior:

https://apcalckellyanderika.wikispaces.com/file/view/vert_asy.gif/206449186/vert_asy.gif

Oscillating Behavior:

http://webpages.charter.net/mwhitneyshhs/calculus/limits/limit-graph8.jpg

 

 

 

 

 

 

 

3.Evaluating Limits:

 -Limits can be evaluated numerically, graphically and algebraically. To evaluate them numerically we must use a table. To evaluate them graphically a graph must be used and then we must compare the left and right limits. To do it algebraically there are three different ways: direct substitution, factoring, and rationalizing. With direct sub. we plug in number. We can get a numerical answer(#), a zero(0/#), the limit does not exist(#/0), and we can get indeterminate form(0/0). If we get indeterminate form that means we must use the other methods to solve the problem. WE ALWAYS USE DIRECT SUB. FIRST. To use factoring means that direct sub. did not work. We must factor the top and the bottom to cancel out things that give us zeros, then we can use direct sub. Rationalizing is used when we multiply the top and the bottom by the conjugate, when using the conjugate we must switch the middle sign.

BQ#4: Unit T concept 1-3

1. A "normal" tangent graph is uphill because of its asymptotes and the unit circle ratios. The unit circle ratio for tangent is equal to y/x, which means that x has to equal zero in the unit circle. X is also equal to cosine, so that means that cosine has to equal zero. The graphs have to be in between the asymptotes, which for the tangent graph is below the x-axis and then above. So it goes from down to up, which creates a uphill tangent graph.

2. A cotangent graph is downhill because the asymptotes are located at different places than a normal tangent graph. The boundaries are in different places. The ratio for cotangent is x/y/, in which y equals zero. Sine equals zero which puts the boundaries and the graph in different places. The graph has to get close to the asymptote above the x-axis, and close to the asymptote down it.

BQ#3: Unit T Concept 1-3

A. Tangent
-Tangent is related to sine and cosine in the ratios. Tan=sin/cos, tangent is also y/x. Tangent will have asymptotes when x=0. The asymptotes depend or are related to sine and cosine. Depending what cosine is then the graph will have asymptotes. If tangent is undefined then asymptotes exist. If cosine is positive tangent will also be positive and if cosine is negative tangent will be negative and therefore below the x-axis.

B. Cotangent
-The ratio for cotangent is x/y or cosine/sine. The asymptotes for cotangent are different because sine now has to equal zero. Depending if sine is positive or negative the graph will be also positive or negative. The asymptotes are drawn depending on what sine is. The graph depends or what sine is.

C.Secant
-Cosine is positive in the first quadrant so secant is also positive. Secant equals one in this case. The ratio for secant is r/x. Secant will have asymptotes whenever cosine equals zero. The graph for secant will always be drawn at the top of every mountain and at the bottom of every valley of the cosine graph. The graph exist where the asymptotes are and they depend on cosine.

D.Cosecant
-The asymptotes will exist whenever sin(x)=0. Every cosecant graph has to touche the top and bottom of the sine graph. If sine is positive so is cosecant and if sine is negative so is cosecant. The graph is drawn where ever the asymptotes exist which are based on sine. The graph depends on what sine is.

BQ#5: Unit T-Concept 1-3

1. Asymptotes exist when the function is undefined, which means when you divide by zero. The ratios for the trig functions are: sine= y/r, cosine=x/y, cosecant=r/y, secant=r/x, tangent=y/x and cotangent=x/y. Sine and cosine do not have asymptotes because according to the ratios they will be always divided by 1 because r=1. The one creates restrictions for sine and cosine. If they are divided by 1 then they are not undefined. The other trig function can have zero as the denominator because they can be divided by zero since x and y 1 or zero.

BQ#2: Unit T- Intro Info.

A. Periods:
-The period for sine and cosine is 2 pie because they go through one cycle while covering 2 pie units on the x-axis. On the unit circle to repeat a cycle for sine it needs to go around one time which at the end is 2 pie or 360 degrees. It needs to go all the way around to repeat. For cosine it is the same thing on the unit circle one cycle must go through all the quadrants to repeat. If it goes all the way around that means it went around 2 pie around the unit circle. The  period for sine and cosine is based on how many times it went around or how many times it had to go around to repeat.For Tangent and Cotangent it is different because to repeat a cycle on the unit circle it only needs to go around halfway for it to repeat. If it only goes around halfway around the unit circle that distance is only pie. The peiod of pie is pie because it only goes halfway on the unit circle which is pie.

B. Amplitude:
-Sine and Cosine have amplitudes of one because of the Unit circle. The ratio of the unit circle of sine was y/r, r=1, and cosine was x/r. That means that sine and cosine are always divided by one. There are limitations because sine and cosine will never have zero as the denominator. Around the unit circle it always go from zero to one to negative one to zero. The other trig functions have no limits because they can be undefined.

Reflection#1-Unit Q: Veryfying Trig Identities

Reflection:
1. An identity is something that it is always true. To rove an identity we use several steps to prove or show how an equation can equal something else. To verify also means that an equation might have two sides and they must equal. Identities are used to prove how those two sides can equal each other. To verify only one side can be touched as we are trying to prove how it is equal to the other side. To verify we must always try to simplify the equation and have it in its simplest terms so it can equal the other side.

2. I have found it helpful to memorize most of the identities. If i have them  memorized I find it easier to work with problems since i can make connections. I also think it is very helpful to try to turn everything in terms of sine and cosine since most identities have them. It is also helpful to separate if possible and work out one part at a time. I find it helpful to write the problem in a different paper than the one you sure solving in it to make as many changes and corrections. A crucial part is to write what steps we are doing to solve it to follow the thought process of the problem better.

3. When i have to solve a problem, the first thing I do is try to see if everything is in terms in cosine or sine, or if there is a need to change them into sine or cosine. The second thing I do is try to identify the problem and see what i need to do to it to make it work. I later look for any identities that might be possible. The next thing I do is combine or multiply anything that needs to be together. I later move make identities with the pieces I got in the previous step. After I combine everything i check to make sure if i can simplify my answer further or change it to a simpler form.