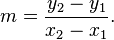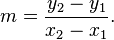BQ#7: Difference Quotient

1.To find the difference quotient we have to get a graph. Then though that graph we draw a line that touches the graph at two point and we call that the secant line. The coordinate for point A(the first point) is (x,f(x)) and point B has coordinates of (x+h,f(x+h)). We need to calculate the slope of the secant line by slope formula which is y2-y1/x2-x1. Y2=f(x+h), Y1=f(x), X2=x+h, X1=x. The equation should be f(x+h)-f(x)/x+h-x. The x's at the bottom cancel leaving the slope to be f(x+h)-f(x)/h, which is the difference quotient formula.

http://cis.stvincent.edu/carlsond/ma109/diffquot.html

http://simple.wikipedia.org/wiki/Difference_quotient

BQ:#6: Unit U Concept 1-7

1. Continuity/Discontinuities:

-A continuous function is predictable. It has no breaks in the graph, no holes, and no jumps. it can be drawn with a single unbroken pencil stoke and it makes a good bridge.
-A discontinuous function can have 3 types of discontinuities, which are in two families. The two families are removable and non-removable discontinuities. In the removable discontinuities there is a Point discontinuity(known as A Hole). In the non-removable discontinuity family there are: jump discontinuities, oscillating behavior, and infinite discontinuities. They are in two families because Removable discontinuities have limits and non-removable discontinuities do not have limits.

Removable discontinuities:

https://centralmathteacher.wikispaces.com/file/view/math1.JPG/30652173/math1.JPG

Non-removable discontinuities:

http://www.math.brown.edu/utra/discontinuities%205.gif

2. Limits:

-A Limit is the intended height of a function. Sometimes the value of a limit is just approached, meaning the graph never reaches it. A limit exist as long as the height is reached from the left and the right. The right hand limit and the left handed limit must be the same. If a graph does not break at any given x-value then a limit exist. A limit can exist even if the destination is a hole in the graph.
-A limit does not exist at three non-removable discontinuities, which are: comparing left and rgiht behavior, unbounded behavior, and oscillating behavior. When comparing left and right they both must approach the number. If the left-handed limit and the right-handed limit are not the same then the limit does not exist. One-handed statements must be written explaining how the left and the right are not the same. Unbounded Behavior exist because of vertical asymptotes. Having vertical asymptotes makes the function approach infinity from the right and negative infinity from the left. When the limit is unbounded because infinity is not a real number. Oscillating behavior is very wiggly at the origin. This type of function does not have a limit because it doesnt approach any single value.

 Left and right Limit notation:

http://www.vias.org/calculus/img/03_continuous_functions-69.gif

Unbounded Behavior:

https://apcalckellyanderika.wikispaces.com/file/view/vert_asy.gif/206449186/vert_asy.gif

Oscillating Behavior:

http://webpages.charter.net/mwhitneyshhs/calculus/limits/limit-graph8.jpg

 

 

 

 

 

 

 

3.Evaluating Limits:

 -Limits can be evaluated numerically, graphically and algebraically. To evaluate them numerically we must use a table. To evaluate them graphically a graph must be used and then we must compare the left and right limits. To do it algebraically there are three different ways: direct substitution, factoring, and rationalizing. With direct sub. we plug in number. We can get a numerical answer(#), a zero(0/#), the limit does not exist(#/0), and we can get indeterminate form(0/0). If we get indeterminate form that means we must use the other methods to solve the problem. WE ALWAYS USE DIRECT SUB. FIRST. To use factoring means that direct sub. did not work. We must factor the top and the bottom to cancel out things that give us zeros, then we can use direct sub. Rationalizing is used when we multiply the top and the bottom by the conjugate, when using the conjugate we must switch the middle sign.

BQ#4: Unit T concept 1-3

1. A "normal" tangent graph is uphill because of its asymptotes and the unit circle ratios. The unit circle ratio for tangent is equal to y/x, which means that x has to equal zero in the unit circle. X is also equal to cosine, so that means that cosine has to equal zero. The graphs have to be in between the asymptotes, which for the tangent graph is below the x-axis and then above. So it goes from down to up, which creates a uphill tangent graph.

2. A cotangent graph is downhill because the asymptotes are located at different places than a normal tangent graph. The boundaries are in different places. The ratio for cotangent is x/y/, in which y equals zero. Sine equals zero which puts the boundaries and the graph in different places. The graph has to get close to the asymptote above the x-axis, and close to the asymptote down it.

BQ#3: Unit T Concept 1-3

A. Tangent
-Tangent is related to sine and cosine in the ratios. Tan=sin/cos, tangent is also y/x. Tangent will have asymptotes when x=0. The asymptotes depend or are related to sine and cosine. Depending what cosine is then the graph will have asymptotes. If tangent is undefined then asymptotes exist. If cosine is positive tangent will also be positive and if cosine is negative tangent will be negative and therefore below the x-axis.

B. Cotangent
-The ratio for cotangent is x/y or cosine/sine. The asymptotes for cotangent are different because sine now has to equal zero. Depending if sine is positive or negative the graph will be also positive or negative. The asymptotes are drawn depending on what sine is. The graph depends or what sine is.

C.Secant
-Cosine is positive in the first quadrant so secant is also positive. Secant equals one in this case. The ratio for secant is r/x. Secant will have asymptotes whenever cosine equals zero. The graph for secant will always be drawn at the top of every mountain and at the bottom of every valley of the cosine graph. The graph exist where the asymptotes are and they depend on cosine.

D.Cosecant
-The asymptotes will exist whenever sin(x)=0. Every cosecant graph has to touche the top and bottom of the sine graph. If sine is positive so is cosecant and if sine is negative so is cosecant. The graph is drawn where ever the asymptotes exist which are based on sine. The graph depends on what sine is.

BQ#5: Unit T-Concept 1-3

1. Asymptotes exist when the function is undefined, which means when you divide by zero. The ratios for the trig functions are: sine= y/r, cosine=x/y, cosecant=r/y, secant=r/x, tangent=y/x and cotangent=x/y. Sine and cosine do not have asymptotes because according to the ratios they will be always divided by 1 because r=1. The one creates restrictions for sine and cosine. If they are divided by 1 then they are not undefined. The other trig function can have zero as the denominator because they can be divided by zero since x and y 1 or zero.

BQ#2: Unit T- Intro Info.

A. Periods:
-The period for sine and cosine is 2 pie because they go through one cycle while covering 2 pie units on the x-axis. On the unit circle to repeat a cycle for sine it needs to go around one time which at the end is 2 pie or 360 degrees. It needs to go all the way around to repeat. For cosine it is the same thing on the unit circle one cycle must go through all the quadrants to repeat. If it goes all the way around that means it went around 2 pie around the unit circle. The  period for sine and cosine is based on how many times it went around or how many times it had to go around to repeat.For Tangent and Cotangent it is different because to repeat a cycle on the unit circle it only needs to go around halfway for it to repeat. If it only goes around halfway around the unit circle that distance is only pie. The peiod of pie is pie because it only goes halfway on the unit circle which is pie.

B. Amplitude:
-Sine and Cosine have amplitudes of one because of the Unit circle. The ratio of the unit circle of sine was y/r, r=1, and cosine was x/r. That means that sine and cosine are always divided by one. There are limitations because sine and cosine will never have zero as the denominator. Around the unit circle it always go from zero to one to negative one to zero. The other trig functions have no limits because they can be undefined.

Reflection#1-Unit Q: Veryfying Trig Identities

Reflection:
1. An identity is something that it is always true. To rove an identity we use several steps to prove or show how an equation can equal something else. To verify also means that an equation might have two sides and they must equal. Identities are used to prove how those two sides can equal each other. To verify only one side can be touched as we are trying to prove how it is equal to the other side. To verify we must always try to simplify the equation and have it in its simplest terms so it can equal the other side.

2. I have found it helpful to memorize most of the identities. If i have them  memorized I find it easier to work with problems since i can make connections. I also think it is very helpful to try to turn everything in terms of sine and cosine since most identities have them. It is also helpful to separate if possible and work out one part at a time. I find it helpful to write the problem in a different paper than the one you sure solving in it to make as many changes and corrections. A crucial part is to write what steps we are doing to solve it to follow the thought process of the problem better.

3. When i have to solve a problem, the first thing I do is try to see if everything is in terms in cosine or sine, or if there is a need to change them into sine or cosine. The second thing I do is try to identify the problem and see what i need to do to it to make it work. I later look for any identities that might be possible. The next thing I do is combine or multiply anything that needs to be together. I later move make identities with the pieces I got in the previous step. After I combine everything i check to make sure if i can simplify my answer further or change it to a simpler form.

SP#7: Unit Q Concept 3: Trigonometry substitution

Please see my SP7, made in collaboration with Kenia G., by visiting their blog here. Also be sure to check out the other awesome posts on their blog.

I/D# 3: Unit Q- Phytagorean Identities

INQUIRY ACTIVITY SUMMARY:

1. An identity is a proven fact that is always true. The Pythagorean Theorem is an identity because it can be proven that a squared plus b squared will equal c squared. In terms of x, y, and r as used in the Unit circle, the Pythagorean theorem is x^2+y^2=r^2. If we try to get the Pythagorean Theorem in terms of x,y, and r equal one, we must divide by r^2. The equation that results is (x/r)^2+(y/r)^2=1. The ratio for cosine on the unit circle is x/y and the ratio for sine on the Unit circle is y/r. If (y/r)^2 is replaced by sine is the equation it will be sin^2 and (x/r)^2 is replaced by cosine it will be cos^2. The equation will end up being sin^2x+cos^2=1. 

2. To derive the rest of the remaining identities we must divide different things to get them. We also must use our ratio identities and reciprocal identities to find them.

 INQUIRY ACTIVITY REFLECTION:
1.The connections that I see between Units N, O, P, Q are that they all use the Unit Circle as a basis to derive different equations. They also use the Magic Tree to  derive certain equations.
 

WPP# 13-14: Unit P Concept 6-7

                                      

                            Please see my WPP13-14, made in collaboration with Kenia G. Please visit the other awesome post on their blog by going here.
                                                           The Problem:

a) Danielle is due east from an oak tree. Danielle is looking at Andrew at a bearing of S32W. Andrew is looking at the same oak tree with a bearing of N15E. Andrew is also 52 feet away from the oak tree. How many feet apart are Andrew and Danielle?

b) Andrew and Danielle are now together and they go on a date. Sadly the time for them to be apart has come. They leave the same point. Their paths diverge at a bearing of 088 degrees. If Danielle walks 2.7 miles and Andrew walks 3 miles,how far apart are they at this time?


                                                                            The Solution:

BQ#1: Unit P Concept 1-5- Law of Sines AAS or ASA, Area of an oblique triangle.

1. Law Of Sines-

     The law of sines is needed when you are not working with a non-right triangles. This helps us with  the trig functions that are used for solving non-right triangles.
How is derived:
1.)

To create a right triangle we must drop a perpendicular line from angle B and it can be labeled as h.  Two right triangles are now created. To use the law of sines, two sides and two angles must be present.

2)

To find the missing parts of a triangle the following relationships are needed.  To find h you can use the transitive property and have cSineA=aSineC, since they both equal h.

3)

If you divide both side by ac then SinA/a= SinC/ c. This is one of the relationships used in the law of sines. The ratios can be used to find any parts of a non-right triangle.

4. Areas formulas: 

The area of an oblique triangle cannot be found without the value of h. The area of a right triangle is A= 1/2bh, where b is the base and h is the height of the triangle.

In this triangle sinC=h/a and we know that h=asinc. We substitute h for asinc in the are formula which is A=1/2bh. The new formula is A=1/2b(asinc) The area of an oblique triangle is one half of the product of two sides and the sine of the given angle. The angle that we are trying to find must be in between the two sides that were given. Two sides and a angle must always be present. The angle will always be sine of the given angle.

WPP#12: Unit O Concept 10

Create your own Playlist on LessonPaths!

1/D: #2 Unit O Concept 7-8: Derive the SRTs

Inquiry Summary Activity:

 To derive the Special Right Triangles, I started with a square with the side lengths of one and a equilateral triangle with the side lengths of 1. Theses two shapes help us derive the 45-45-90 Special Triangle and the 30-60-90 Special Triangle.The Pythagorean Theorem was also used to find missing parts of the triangles.

1) 30-60-90 Triangle:
To derive the 30-60-90 triangle,  I used a equilateral triangle with the side lengths of 1. An equilateral triangle has angles that are 60 degrees and all 3 angles are the same. Since a equilateral triangle has the same angles and the same sides, I sliced it down the middle. By slicing it down the middle a height and a 90 degree angle were created. A 30 degree angle was also created by splitting the 60 degree angle in half. Since the triangle was sliced now the base is 1/2. Since we know that on side is 1 and the base is now 1/2, using the Pythagorean Theorem we can figure what the height is. We use the a^2+b^2=c^2. a=One squared is a=1 and b=1/2 squared is b= 1/4. You add them and that gives radical 3 over 2.We multiply everything by 2 to get radical 3, 2 and 1. This translates into the normal n radical3, 2n, and n. The n is used as variable meaning that any number can be substituted in. N is used to expand the problem as needed.

2) 45-45-90 Triangle:
To derive the 45-45-90 triangle, I used a square with the sides of 1. The 4 angles of a square are 90 degrees.I sliced the square down its diagonal. By cutting it down its diagonal created  a hypotenuse and two 45 degree angles. Since we know that two sides are 1 we must now find the hypotenuse of the triangle created. I used the Pythagorean Theorem to find the hypotenuse. The equation is a^2+b^2=c^2. A=1 and B=1, which means c stays the same. 1 squared is 1 so that means a+b equals one. To get c we must get rid of the square root by squaring c and 2. That means c equals radical 2. The sides of the triangle are 1,1, and radical 2. That translates to the original pattern of a 45-45-90 triangle which is: n,n, n radical 2. The N is used a variable, which means any number can be substituted and that means that N is also used to expand the problem as needed.

Inquiry Activity Reflection:
1) Something I never noticed before about special right triangles is that they were created form other shapes.
2)Being able to derive these patterns myself aids my learning because if I need to do a problem that involves this and the triangles are not given I can do it on my own.

I/D#1:Unit N Concept 7: Derive the Unit Circle Activity

Inquiry Activity Summary:

In this activity we were given 3 triangles which had the measurements of: 30, 60,90, 45,45,90 and 60,30, and 90 degrees. These measurements are of Special Right Triangles. We had to label each triangle according to the rules of Special Triangles. Which are:

http://www.math.hmc.edu/calculus/tutorials/reviewtriglogexp/Add caption

The hypotenuse of each triangle had to equal 1. The first triangle was a 30 degree which meant that the sides where labeled as 2x, x radical 3, and x. To make the hypotenuse 1, we had to dive all sides by the hypotenuse and simplify. After that we labeled the hypotenuse "r", horizontal value"x", and vertical value "y". The next step is to draw a coordinate(this has to be done to very triangle given) with the origin at the labeled measure, which for the first one was 30 degrees. The vertices had to be labeled as ordered pairs for each triangle. For the first triangle, which is 30 degrees, The hypotenuse equal 2x(r), and the sides were x(vertical value), and x radical 3(horizontal value). To simplify I had to divide all sides by 2x, which gave me 1 for the r value, radical 3 over 2 for x, and 1/2 for y. I later drew the coordinate and labeled the order pairs which were (0,0), (radical 3/2,0), and (radical 3/2, 1/2). That is how the ordered pairs that are in the Unit Circle came to be for any reference angle of 30. The pairs are the same for any reference angle of 30.
1)30 Degree Triangle:

2) 45 Degree Triangle:
For the 45 degree angle, the hypotenuse was x radical 2(R), vertical side was x(x), and horizontal side was x(Y). For this triangle we had to divide by radical 2, which gave R=1, X= radical 2/2, and Y= radical2/2. After drawing the coordinate plane, the vertices were: (0,0), (radical 2 over 2, 0), and (radical 2 over 2, radical 2 over 2). That is how the ordered pairs for the quadrants in the unit circle came from, for angles that were reference angles of 45 degrees.

3) 60 Degree Triangle:
For the 60 degree triangle, the hypotenuse was 2x(R), horizontal side was x(x), and vertical side was x radical 3(y). We had to divide by 2x which gave r=1, x=1/2, and y= radical 3 over 2. After drawing the coordinate plane, the vertices were (0,0), (1/2,0), and (1/2, radical 3 over 2). That is how the pairs for any reference angle of 60 came to be. For any reference angle of 60 in the unit circle the pairs will be the same.

4) This activity helps us obtain the unit circle because the ordered pairs that we got for the tree triangles are the same in each quadrant of the unit circle, which means that if you know the pairs for the 30, 45, and 60 degree angles you will know the complete unit circle. As each of the tree angles have reference angles in each quadrant.

5)The triangles drawn lie in the first quadrant, which makes the ordered pairs positive. If the triangles were drawn in different quadrants the pairs would change to negative depending in what quadrant they are. After re-drawing the triangles, for the 30 degree triangle in the second quadrant, the x values of the ordered pair became negative. For the 45 degree triangle the x and y values both became negative in the third quadrant. For the 60 degree triangle the y values became negative when drawn in the fourth quadrant.

Inquiry Activity Reflection:

1. "The coolest thing I learned from this activity was" where the unit circle came from.
2. "This activity will help me in this unit because" it will help be get reference angles faster and the ordered pairs.
3. "Something I never realized about special right triangles and the unit circle was" that they had so much in common or that the triangles were used to make the unit circle.

RWA#1: Unit M Concept 5: Graphing ellipses given equation

  

 Section 1:

• The set off all points, such that the sum of the distance known as the foci, is constant.
• Equation: (x-h)^2 / a^2 + (y-k)^2 / b^2=1 or (x-h)^2 / b^2 + (y-k)^2 / a^2=1 and a^2-b^2=c^2
• The key points of an ellipse are: the center, a, b, c, 2 vertices, the major axis, 2 co-vertices, the minor axis, 2 foci, and the eccentricity. To find A and B is the standard form is given A will always be the bigger number. Depending if x or y come first the graph will be either skinny or fat. If Its skinny the x value will not change from the center. to get the vertices, if its skinny the x values wont change and you will need to add and subtract whatever number a  is to find the y values. For the co-vertices the y will be the same as the center and subtract and add whatever number b is to find the x values. The major axis will depend on if its skinny or fat, if its skinny major axis will be x= whatever number x is for the center and the minor axis will equal whatever y is in the center. For a fat graph the numbers will change y will become major and x minor. To find the foci you need to know c and depending if its skinny or fat the x or y values will change from the numbers that make up the center. To find C you use  a^2-b^2 =c^2. The eccentricity will be C over A.

The closer the foci are to the vertices the ellipse will become fat and the closer they are to the center it will become more narrow or skinny.


Section 3:
A real world application that displays ellipses are earrings. Earrings can be worn on the ears and can be different material and color. Earrings can be in the form of ellipses.Most women over the world use earring. This real world application contains different sizes for ellipses.

Section 4:
http://www.mathamazement.com/Lessons/Pre-Calculus/09_Conic-Sections-and-Analytic-Geometry/ellipse.html
http://official-stardollfashion.blogspot.com/2009/06/8-hottest-trends-for-summer-2009.html

WPP#10:UNIT L Concept 9-14

Create your own Playlist on LessonPaths!